Conische doorsnede, ook wel conisch genoemd, in geometrie, elke curve die wordt geproduceerd door het snijpunt van een vlak en een rechtse cirkelvormige kegel. Afhankelijk van de hoek van het vlak ten opzichte van de kegel, is het snijpunt een cirkel, een ellips, een hyperbool of een parabool. Speciale (gedegenereerde) gevallen van kruising treden op wanneer het vlak alleen door de top gaat (een enkel punt produceert) of door de top en een ander punt op de kegel (een rechte lijn of twee kruisende rechte lijnen produceert). Zie de figuur.
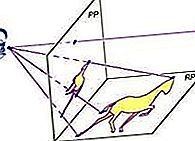
projectieve geometrie: projectieve kegelsneden
Conische secties kunnen worden beschouwd als vlakke secties van een rechter cirkelvormige kegel (zie de afbeelding). Door te kijken
De basisbeschrijvingen, maar niet de namen, van de kegelsnedes zijn terug te voeren op Menaechmus (bloeide rond 350 voor Christus), een leerling van zowel Plato als Eudoxus van Cnidus. Apollonius van Perga (ca. 262–190 v.Chr.), Bekend als de "Grote Geometer", gaf de kegelsneden hun naam en was de eerste die de twee takken van de hyperbool definieerde (die de dubbele kegel veronderstelt). Apollonius 'achtdelige verhandeling over de kegelsneden, Conics, is een van de grootste wetenschappelijke werken uit de oudheid.
Analytische definitie
Conics kunnen ook worden beschreven als vlakke krommen die de paden (loci) zijn van een punt dat zo beweegt dat de verhouding van de afstand van een vast punt (de focus) tot de afstand van een vaste lijn (de richtlijn) een constante is, genaamd de excentriciteit van de curve. Als de excentriciteit nul is, is de curve een cirkel; indien gelijk aan één, een parabool; indien minder dan één, een ellips; en indien groter dan één, een hyperbool. Zie de figuur.
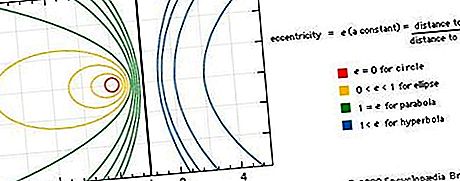
Elke kegelsnede komt overeen met de grafiek van een tweedegraads polynoomvergelijking van de vorm Ax 2 + By 2 + 2Cxy + 2Dx + 2Ey + F = 0, waarbij x en y variabelen zijn en A, B, C, D, E en F zijn coëfficiënten die afhankelijk zijn van de specifieke kegelsnede. Door een geschikte keuze van coördinaatassen kan de vergelijking voor elke kegelsnede worden teruggebracht tot een van de drie eenvoudige r-vormen: x 2 / a 2 + y 2 / b 2 = 1, x 2 / a 2 - y 2 / b 2 = 1, of y 2 = 2 px, wat respectievelijk overeenkomt met een ellips, een hyperbool en een parabool. (Een ellips waarbij a = b in feite een cirkel is.) Het uitgebreide gebruik van coördinatensystemen voor de algebraïsche analyse van geometrische krommen is ontstaan bij René Descartes (1596–1650). Zie Geschiedenis van geometrie: Cartesiaanse geometrie.
Griekse afkomst
De vroege geschiedenis van kegelsneden gaat samen met het probleem van "verdubbeling van de kubus". Volgens Eratosthenes van Cyrene (ca. 276–190 v.Chr.) Raadpleegden de mensen van Delos het orakel van Apollo voor hulp bij het beëindigen van een plaag (ca. 430 v.Chr.) En kregen de opdracht Apollo een nieuw altaar te bouwen van tweemaal het volume van het oude altaar. en met dezelfde kubusvorm. Perplex raadpleegde de Deliërs Plato, die zei dat 'het orakel niet betekende dat de god een dubbel zo groot altaar wilde, maar dat hij, door hen de taak te stellen, de Grieken wilde beschamen omdat ze de wiskunde negeerden en minachtten voor geometrie. ' Hippocrates of Chios (c. 470–410 bc) ontdekte voor het eerst dat het "Delian-probleem" kan worden teruggebracht tot het vinden van twee gemiddelde verhoudingen tussen a en 2a (de volumes van de respectievelijke altaren) - dat wil zeggen, het bepalen van x en y zodat een: x = x: y = y: 2a. Dit komt overeen met het oplossen van twee willekeurige vergelijkingen x 2 = ay, y 2 = 2ax en xy = 2a 2, die respectievelijk overeenkomen met twee parabolen en een hyperbool. Later toonden Archimedes (ca. 290–211 v. Chr.) Aan hoe kegelvormige secties kunnen worden gebruikt om een bol in twee segmenten met een bepaalde verhouding te verdelen.
Diocles (ca. 200 v.Chr.) Toonden geometrisch aan dat stralen - bijvoorbeeld van de zon - die evenwijdig zijn aan de as van een omwentelingsparaboloïde (geproduceerd door een parabool rond zijn symmetrieas te draaien) elkaar raken in het brandpunt. Archimedes zou deze eigenschap hebben gebruikt om vijandelijke schepen in brand te steken. De brandpuntseigenschappen van de ellips werden aangehaald door Anthemius van Tralles, een van de architecten voor de Hagia Sophia-kathedraal in Constantinopel (voltooid in AD 537), om ervoor te zorgen dat een altaar de hele dag door zonlicht kon worden verlicht.













