Differentiaalvergelijkingeen wiskundige verklaring die een of meer afgeleiden bevat, dat wil zeggen termen die de veranderingssnelheden van continu variërende hoeveelheden vertegenwoordigen. Differentiaalvergelijkingen zijn heel gebruikelijk in wetenschap en techniek, evenals in vele andere gebieden van kwantitatieve studie, omdat wat direct kan worden waargenomen en gemeten voor systemen die veranderingen ondergaan, hun veranderingssnelheid is. De oplossing van een differentiaalvergelijking is in het algemeen een vergelijking die de functionele afhankelijkheid van één variabele van één of meer andere uitdrukt; het bevat normaal gesproken constante termen die niet aanwezig zijn in de oorspronkelijke differentiaalvergelijking. Een andere manier om dit te zeggen is dat de oplossing van een differentiaalvergelijking een functie oplevert die kan worden gebruikt om het gedrag van het oorspronkelijke systeem te voorspellen, althans binnen bepaalde beperkingen.

analyse: Newton en differentiaalvergelijkingen
de toepassing van analyse zijn differentiaalvergelijkingen, die de veranderingssnelheden van verschillende grootheden relateren aan hun huidige waarden,
Differentiaalvergelijkingen zijn onderverdeeld in verschillende brede categorieën en deze zijn op hun beurt verder onderverdeeld in vele subcategorieën. De belangrijkste categorieën zijn gewone differentiaalvergelijkingen en partiële differentiaalvergelijkingen. Wanneer de functie die betrokken is bij de vergelijking afhankelijk is van slechts een enkele variabele, zijn de afgeleiden daarvan gewone afgeleiden en wordt de differentiaalvergelijking geclassificeerd als een gewone differentiaalvergelijking. Aan de andere kant, als de functie afhangt van verschillende onafhankelijke variabelen, zodat de afgeleiden partiële afgeleiden zijn, wordt de differentiaalvergelijking geclassificeerd als een partiële differentiaalvergelijking. Hieronder volgen voorbeelden van gewone differentiaalvergelijkingen:
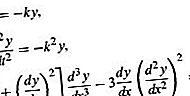
Hierin staat y voor de functie en is t of x de onafhankelijke variabele. De symbolen k en m worden hier gebruikt om te staan voor specifieke constanten.
Wat het type ook is, een differentiaalvergelijking is van de nde orde als het een afgeleide van de nde orde betreft, maar geen afgeleide van een hogere orde. De vergelijking is een voorbeeld van een partiële differentiaalvergelijking van de tweede orde. De theorieën van gewone en partiële differentiaalvergelijkingen zijn duidelijk verschillend, en daarom worden de twee categorieën afzonderlijk behandeld.
In plaats van een enkele differentiaalvergelijking kan het onderzoeksobject een gelijktijdig systeem van dergelijke vergelijkingen zijn. De formulering van de wetten van de dynamiek leidt vaak tot dergelijke systemen. In veel gevallen is een enkele differentiaalvergelijking van de nde orde met voordeel vervangbaar door een systeem van n gelijktijdige vergelijkingen, die elk van de eerste orde zijn, zodat technieken uit lineaire algebra kunnen worden toegepast.
Een gewone differentiaalvergelijking waarin bijvoorbeeld de functie en de onafhankelijke variabele worden aangeduid met y en x is in feite een impliciete samenvatting van de essentiële kenmerken van y als functie van x. Deze kenmerken zouden vermoedelijk beter toegankelijk zijn voor analyse als er een expliciete formule voor y zou kunnen worden geproduceerd. Een dergelijke formule, of in ieder geval een vergelijking in x en y (zonder afgeleiden) die af te leiden is van de differentiaalvergelijking, wordt een oplossing van de differentiaalvergelijking genoemd. Het proces van het afleiden van een oplossing uit de vergelijking door de toepassingen van algebra en calculus wordt het oplossen of integreren van de vergelijking genoemd. Er moet echter worden opgemerkt dat de differentiaalvergelijkingen die expliciet kunnen worden opgelost, maar een kleine minderheid vormen. Daarom moeten de meeste functies worden bestudeerd met indirecte methoden. Zelfs het bestaan ervan moet worden bewezen wanneer er geen mogelijkheid is om het voor inspectie te produceren. In de praktijk worden methoden uit numerieke analyse, waarbij computers betrokken zijn, gebruikt om bruikbare benaderende oplossingen te verkrijgen.













