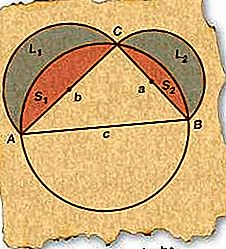
Hippocrates of Chios (fl. C. 460 bc) toonde aan dat de maanvormige gebieden tussen cirkelvormige bogen, bekend als lunes, precies konden worden uitgedrukt als een rechtlijnig gebied of kwadratuur. In het volgende eenvoudige geval hebben twee rond de zijden van een rechthoekige driehoek ontwikkelde lunes een gecombineerd gebied dat gelijk is aan dat van de driehoek.
-
Begin met de juiste ΔABC en teken een cirkel waarvan de diameter samenvalt met AB (zijde c), de hypotenusa. Omdat elke rechthoekige driehoek getekend met de diameter van een cirkel voor zijn hypotenusa moet worden ingeschreven binnen de cirkel, moet C op de cirkel staan.
-
Teken halve cirkels met diameters AC (zijde b) en BC (zijde a) zoals in de figuur.
-
Label de resulterende lunes L 1 en L 2 en de resulterende segmenten S 1 en S 2, zoals aangegeven in de afbeelding.
-
Nu moet de som van de lunes (L 1 en L 2) gelijk zijn aan de som van de halve cirkels (L 1 + S 1 en L 2 + S 2) die ze bevatten minus de twee segmenten (S 1 en S 2). Dus L 1 + L 2 = π / 2 (b / 2) 2 - S 1 + π / 2 (a / 2) 2 - S 2 (aangezien de oppervlakte van een cirkel π maal het kwadraat van de straal is).
-
De som van de segmenten (S 1 en S 2) is gelijk aan de oppervlakte van de halve cirkel gebaseerd op AB minus de oppervlakte van de driehoek. Aldus S 1 + S 2 = π / 2 (c / 2) 2 - ΔABC.
-
Vervanging van de uitdrukking in stap 5 in stap 4 en rekening houdend met algemene termen, L 1 + L 2 = π / 8 (a 2 + b 2 - c 2) + ΔABC.
-
Aangezien ∠ACB = 90 °, a 2 + b 2 - c 2 = 0, volgens de stelling van Pythagoras. Aldus L 1 + L 2 = ΔABC.
Hippocrates slaagde erin verschillende soorten lunes te kwadrateren, sommige op bogen die groter en kleiner waren dan halve cirkels, en hij liet doorschemeren, hoewel hij misschien niet geloofd had, dat zijn methode een hele cirkel kon kwadrateren. Aan het einde van het klassieke tijdperk zei Boethius (c. Ad 470–524), wiens Latijnse vertalingen van fragmenten van Euclid het licht van de geometrie gedurende een half millennium zouden laten flikkeren, dat iemand het kwadrateren van de cirkel had bereikt. Of het onbekende genie lunes gebruikte of een andere methode is niet bekend, omdat Boethius bij gebrek aan ruimte de demonstratie niet gaf. Zo bracht hij de uitdaging van de kwadratuur van de cirkel over, samen met fragmenten van geometrie die blijkbaar nuttig waren bij het uitvoeren ervan. Europeanen hielden de ongelukkige taak tot ver in de Verlichting vol. Uiteindelijk, in 1775, weigerde de Academie van Wetenschappen van Parijs, de taak om de drogredenen te herkennen in de vele oplossingen die haar werden voorgelegd, verder niets te maken te hebben met cirkelvierkanten.